| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 5.1 | Exercise 5.2 | Exercise 5.3 |
| Exercise 5.4 | Exercise 5.5 | Exercise 5.6 |
| Exercise 5.7 | Exercise 5.8 | Exercise 5.9 |
Chapter 5 Understanding Elementary Shapes
The solutions for Chapter 5, "Understanding Elementary Shapes," build upon the basic geometrical ideas by introducing measurement and classification of shapes. This chapter covers measuring line segments, comparing angles, different types of angles (acute, obtuse, right, straight, reflex), perpendicular lines, classification of triangles (based on sides: equilateral, isosceles, scalene; based on angles: acute-angled, obtuse-angled, right-angled), classification of quadrilaterals (parallelogram, rectangle, square, rhombus, trapezium), identification of polygons, and basic concepts of three-dimensional shapes (faces, edges, vertices).
The solutions guide students on how to compare line segments by observation, tracing, or using a ruler and divider. They explain angle measurement using degrees and the concept of a revolution ($360^\circ$). Solutions demonstrate how to classify angles based on their measure and relate them to directions (North, South, East, West) and clock hands. The concept of perpendicular lines (forming a right angle) is explained.
A significant part of the solutions focuses on classifying triangles based on given side lengths or angle measures, reinforcing the definitions and properties of each type. Similarly, solutions help students identify different types of quadrilaterals based on their properties related to sides and angles. The naming and identification of various polygons based on their number of sides (pentagon, hexagon, octagon, etc.) are covered.
Finally, the chapter introduces 3D shapes like cubes, cuboids, spheres, cylinders, cones, and pyramids. The solutions help students visualize these shapes and identify their faces (flat surfaces), edges (where faces meet), and vertices (corners). Exercises involving matching shapes to their names or counting their faces, edges, and vertices are solved clearly. The solutions often use diagrams and property lists to aid understanding, bridging the gap between abstract definitions and concrete shapes, enhancing spatial reasoning and measurement skills.
Exercise 5.1
Question 1. What is the disadvantage in comparing line segments by mere observation?
Answer:
Comparing line segments by mere observation involves looking at the segments and visually judging which one is longer or shorter without using any measuring tools.
The primary disadvantage of this method is the high chance of error.
Human visual perception can be deceptive, especially when the difference in the lengths of the line segments is very small or negligible.
This often leads to inaccurate conclusions about which segment is longer or if they are equal in length.
Therefore, comparing line segments solely by observation is not a reliable or precise method for accurate geometric work.
Question 2. Why is it better to use a divider than a ruler, while measuring the length of a line segment?
Answer:
When measuring the length of a line segment using a ruler, there are potential sources of error:
1. Thickness of the ruler: The markings on a ruler have a certain thickness. It can be difficult to read the measurement accurately because of this thickness.
2. Positioning error (Parallax error): Angular viewing, or not placing your eye directly perpendicular to the mark on the ruler, can lead to incorrect readings. This is known as parallax error.
Using a divider helps to minimize these errors:
1. The divider has two sharp end points. Place one end point at the beginning of the line segment and open the divider such that the other end point is exactly at the end of the line segment.
2. Then, lift the divider carefully without disturbing its opening, and place one of its end points on the '0' mark of the ruler.
3. Read the mark on the ruler where the other end point of the divider rests. This reading gives the length of the line segment.
This method avoids issues related to the ruler's thickness directly affecting the reading against the line segment and reduces the possibility of parallax error while aligning the divider on the ruler.
Therefore, using a divider generally allows for a more accurate measurement of a line segment compared to using a ruler directly.
Question 3. Draw any line segment, say $\overline{AB}$. Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AB = AC + CB?
[Note: If A,B,C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B.]
Answer:
Steps:
1. Draw a line segment: Using a ruler, draw a line segment and name its endpoints A and B. Let's say we draw a line segment $\overline{AB}$ of length 7 cm.
2. Mark a point C: Take any point C lying on the line segment, in between points A and B.
3. Measure the lengths: Use the ruler to measure the lengths of the segments $\overline{AC}$, $\overline{CB}$, and the total segment $\overline{AB}$.
Let's assume our measurements from the diagram are:
Length of $\overline{AB}$ = 7 cm
Length of $\overline{AC}$ = 3 cm
Length of $\overline{CB}$ = 4 cm
Verification:
Now, we need to check if the length of the whole segment is equal to the sum of the lengths of its parts. Is $AB = AC + CB$?
Let's calculate the sum on the right side of the equation:
$AC + CB = 3 \text{ cm} + 4 \text{ cm} = 7 \text{ cm}$
The measured length of $AB$ is also 7 cm.
Since both values are equal, we can conclude:
Yes, $AB = AC + CB$.
Conclusion:
This experiment confirms that if a point C lies between two points A and B on a line segment, the length of the entire segment $\overline{AB}$ is equal to the sum of the lengths of the smaller segments $\overline{AC}$ and $\overline{CB}$. This demonstrates a fundamental property of collinear points.
Question 4. If A,B,C are three points on a line such that AB = 5 cm, BC = 3 cm and AC = 8 cm, which one of them lies between the other two?
Answer:
Given:
We are given three points A, B, and C on a line.
The distances between these points are:
$AB = 5$ cm
$BC = 3$ cm
$AC = 8$ cm
To Find:
Which of the three points lies between the other two.
Solution:
For three collinear points, one point lies between the other two if the sum of the distances between that point and the other two points is equal to the distance between those two outer points.
We need to check which combination of segment lengths adds up to the length of the longest segment.
The lengths given are 5 cm, 3 cm, and 8 cm. The longest segment length is $AC = 8$ cm.
Let's check if the sum of the other two lengths ($AB$ and $BC$) is equal to the length of the longest segment ($AC$).
Calculate the sum $AB + BC$:
$AB + BC = 5 \text{ cm} + 3 \text{ cm} = 8 \text{ cm}$
We are given that $AC = 8$ cm.
Comparing the sum $AB + BC$ with the length $AC$, we find:
$AB + BC = 8 \text{ cm} = AC$
(Using the given values)
Since the condition $AB + BC = AC$ is satisfied, the point that is common to the segments $\overline{AB}$ and $\overline{BC}$ must lie between the points A and C.
The common point is B.
Conclusion:
Therefore, based on the given lengths, point B lies between points A and C.
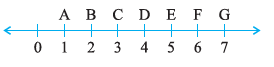
Answer:
Given:
A line segment represented on a number line with points A, B, C, D, E, F, G marked at consecutive integers starting from 1.
From the image, we can determine the positions of points A, D, and G:
Point A is at position 1.
Point D is at position 4.
Point G is at position 7.
To Verify:
Whether D is the midpoint of the line segment $\overline{AG}$.
Solution:
For D to be the midpoint of $\overline{AG}$, the distance from A to D must be equal to the distance from D to G. That is, we need to check if $AD = DG$.
Let's calculate the lengths of the segments $\overline{AD}$ and $\overline{DG}$ based on their positions on the number line.
The length of a segment on the number line is the absolute difference between the coordinates of its endpoints.
Length $AD = (\text{Position of D}) - (\text{Position of A})$
$AD = 4 - 1 = 3$ units.
Length $DG = (\text{Position of G}) - (\text{Position of D})$
$DG = 7 - 4 = 3$ units.
Now, we compare the lengths $AD$ and $DG$.
$AD = 3 \text{ units}$
$DG = 3 \text{ units}$
Since $AD = DG = 3$ units, the point D divides the segment $\overline{AG}$ into two equal parts.
Conclusion:
As the distance $AD$ is equal to the distance $DG$, the point D is indeed the midpoint of the line segment $\overline{AG}$.
The verification is successful.
Question 6. If B is the mid point of $\overline{AC}$ and C is the mid point of $\overline{BD}$, where A, B, C, D lie on a straight line, say why AB = CD?
Answer:
Given:
1. Points A, B, C, and D lie on a straight line.
2. B is the midpoint of the line segment $\overline{AC}$.
3. C is the midpoint of the line segment $\overline{BD}$.
To Prove:
The length of segment $\overline{AB}$ is equal to the length of segment $\overline{CD}$, i.e., $AB = CD$.
Proof:
Since B is the midpoint of $\overline{AC}$, it means that B divides the segment $\overline{AC}$ into two segments of equal length.
$AB = BC$
[Definition of midpoint] ... (i)
Similarly, since C is the midpoint of $\overline{BD}$, it means that C divides the segment $\overline{BD}$ into two segments of equal length.
$BC = CD$
[Definition of midpoint] ... (ii)
Now, we compare equation (i) and equation (ii).
From (i), we have the length $AB$ is equal to the length $BC$.
From (ii), we have the length $BC$ is equal to the length $CD$.
Using the transitive property of equality (if $a=b$ and $b=c$, then $a=c$), we can combine equations (i) and (ii):
Since $AB = BC$ and $BC = CD$, it follows that:
$AB = CD$
Thus, it is proven that the length of segment $\overline{AB}$ is equal to the length of segment $\overline{CD}$.
Question 7. Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Answer:
Procedure:
We will draw five different triangles, measure their sides, and check in each case if the sum of the lengths of any two sides is always less than the third side, as the question asks.
Triangle 1: A Scalene Triangle
The measured side lengths are $a = 4$ cm, $b = 6$ cm, and $c = 7$ cm.
Checks:
Is $4 + 6 < 7$? Is $10 < 7$? No.
Is $4 + 7 < 6$? Is $11 < 6$? No.
Is $6 + 7 < 4$? Is $13 < 4$? No.
Triangle 2: An Isosceles Triangle
The measured side lengths are $a = 5$ cm, $b = 5$ cm, and $c = 3$ cm.
Checks:
Is $5 + 5 < 3$? Is $10 < 3$? No.
Is $5 + 3 < 5$? Is $8 < 5$? No.
Triangle 3: A Right-Angled Triangle
The measured side lengths are $a = 3$ cm, $b = 4$ cm, and $c = 5$ cm.
Checks:
Is $3 + 4 < 5$? Is $7 < 5$? No.
Is $3 + 5 < 4$? Is $8 < 4$? No.
Is $4 + 5 < 3$? Is $9 < 3$? No.
Triangle 4: An Obtuse-Angled Triangle
The measured side lengths are $a = 5$ cm, $b = 8$ cm, and $c = 11$ cm.
Checks:
Is $5 + 8 < 11$? Is $13 < 11$? No.
Is $5 + 11 < 8$? Is $16 < 8$? No.
Is $8 + 11 < 5$? Is $19 < 5$? No.
Triangle 5: An Equilateral Triangle
The measured side lengths are $a = 6$ cm, $b = 6$ cm, and $c = 6$ cm.
Checks:
Is $6 + 6 < 6$? Is $12 < 6$? No.
Observation:
In all five cases, for every combination of two sides, their sum was not less than the third side. The condition stated in the question ("sum of the lengths of any two sides is always less than the third side") is false.
Conclusion:
The investigation shows that the premise of the question is incorrect. There is a well-known property of triangles called the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
For a triangle with side lengths $a$, $b$, and $c$, the following inequalities are always true:
$a + b > c$
$a + c > b$
$b + c > a$
Thus, our experiment confirms that the sum of the lengths of any two sides of a triangle is never less than the third side; it is always greater.
Exercise 5.2
Question 1. What fraction of a clockwise revolution does the hour hand of a clock turn through, when it goes from
(a) 3 to 9
(b) 4 to 7
(c) 7 to 10
(d) 12 to 9
(e) 1 to 10
(f) 6 to 3
Answer:
One complete clockwise revolution of the hour hand of a clock covers 12 hours.
The fraction of a revolution is calculated by dividing the number of hours the hand moves clockwise by the total 12 hours.
(a) 3 to 9
The hour hand moves clockwise from 3 to 9.
Number of hours moved = $9 - 3 = 6$ hours.
Fraction of revolution = $\frac{\text{Hours moved}}{\text{Total hours in one revolution}} = \frac{6}{12}$
Simplifying the fraction: $\frac{6}{12} = \frac{\cancel{6}^1}{\cancel{12}_2} = \frac{1}{2}$
So, the fraction is $\frac{1}{2}$.
(b) 4 to 7
The hour hand moves clockwise from 4 to 7.
Number of hours moved = $7 - 4 = 3$ hours.
Fraction of revolution = $\frac{3}{12}$
Simplifying the fraction: $\frac{3}{12} = \frac{\cancel{3}^1}{\cancel{12}_4} = \frac{1}{4}$
So, the fraction is $\frac{1}{4}$.
(c) 7 to 10
The hour hand moves clockwise from 7 to 10.
Number of hours moved = $10 - 7 = 3$ hours.
Fraction of revolution = $\frac{3}{12}$
Simplifying the fraction: $\frac{3}{12} = \frac{\cancel{3}^1}{\cancel{12}_4} = \frac{1}{4}$
So, the fraction is $\frac{1}{4}$.
(d) 12 to 9
The hour hand moves clockwise from 12 to 9.
Number of hours moved = 9 hours (from 12 to 1, 1 to 2, ..., 8 to 9).
Fraction of revolution = $\frac{9}{12}$
Simplifying the fraction: $\frac{9}{12} = \frac{\cancel{9}^3}{\cancel{12}_4} = \frac{3}{4}$
So, the fraction is $\frac{3}{4}$.
(e) 1 to 10
The hour hand moves clockwise from 1 to 10.
Number of hours moved = $10 - 1 = 9$ hours.
Fraction of revolution = $\frac{9}{12}$
Simplifying the fraction: $\frac{9}{12} = \frac{\cancel{9}^3}{\cancel{12}_4} = \frac{3}{4}$
So, the fraction is $\frac{3}{4}$.
(f) 6 to 3
The hour hand moves clockwise from 6 to 3.
Number of hours moved = (from 6 to 12) + (from 12 to 3) = $(12 - 6) + 3 = 6 + 3 = 9$ hours.
Fraction of revolution = $\frac{9}{12}$
Simplifying the fraction: $\frac{9}{12} = \frac{\cancel{9}^3}{\cancel{12}_4} = \frac{3}{4}$
So, the fraction is $\frac{3}{4}$.
Question 2. Where will the hand of a clock stop if it
(a) starts at 12 and makes $\frac{1}{2}$ of a revolution, clockwise?
(b) starts at 2 and makes $\frac{1}{2}$ of a revolution, clockwise?
(c) starts at 5 and makes $\frac{1}{4}$ of a revolution, clockwise?
(d) starts at 5 and makes $\frac{3}{4}$ of a revolution, clockwise?
Answer:
A clock face is divided into 12 hours. One full revolution corresponds to moving 12 hours.
To find the stopping position, we calculate the number of hours moved for the given fraction of a revolution and add it to the starting position, moving clockwise.
(a) starts at 12 and makes $\frac{1}{2}$ of a revolution, clockwise?
Number of hours in $\frac{1}{2}$ revolution = $\frac{1}{2} \times 12 = 6$ hours.
Starting position: 12
Moving 6 hours clockwise from 12:
12 $\rightarrow$ 1 $\rightarrow$ 2 $\rightarrow$ 3 $\rightarrow$ 4 $\rightarrow$ 5 $\rightarrow$ 6
The hand will stop at 6.
(b) starts at 2 and makes $\frac{1}{2}$ of a revolution, clockwise?
Number of hours in $\frac{1}{2}$ revolution = $\frac{1}{2} \times 12 = 6$ hours.
Starting position: 2
Moving 6 hours clockwise from 2:
2 $\rightarrow$ 3 $\rightarrow$ 4 $\rightarrow$ 5 $\rightarrow$ 6 $\rightarrow$ 7 $\rightarrow$ 8
The hand will stop at 8.
(c) starts at 5 and makes $\frac{1}{4}$ of a revolution, clockwise?
Number of hours in $\frac{1}{4}$ revolution = $\frac{1}{4} \times 12 = 3$ hours.
Starting position: 5
Moving 3 hours clockwise from 5:
5 $\rightarrow$ 6 $\rightarrow$ 7 $\rightarrow$ 8
The hand will stop at 8.
(d) starts at 5 and makes $\frac{3}{4}$ of a revolution, clockwise?
Number of hours in $\frac{3}{4}$ revolution = $\frac{3}{4} \times 12 = 3 \times 3 = 9$ hours.
Starting position: 5
Moving 9 hours clockwise from 5:
5 $\rightarrow$ 6 $\rightarrow$ 7 $\rightarrow$ 8 $\rightarrow$ 9 $\rightarrow$ 10 $\rightarrow$ 11 $\rightarrow$ 12 $\rightarrow$ 1 $\rightarrow$ 2
The hand will stop at 2.
Question 3. Which direction will you face if you start facing
(a) east and make $\frac{1}{2}$ of a revolution clockwise?
(b) east and make $1\frac{1}{2}$ of a revolution clockwise?
(c) west and make $\frac{3}{4}$ of a revolution anti-clockwise?
(d) south and make one full revolution?
(Should we specify clockwise or anti-clockwise for this last question? Why not?)
Answer:
We consider the four main directions: North (N), East (E), South (S), and West (W).
A full revolution is $360^\circ$ or 4 right angles.
A $\frac{1}{2}$ revolution is $180^\circ$ (2 right angles).
A $\frac{1}{4}$ revolution is $90^\circ$ (1 right angle).
A $\frac{3}{4}$ revolution is $270^\circ$ (3 right angles).
Clockwise movement follows the order N $\rightarrow$ E $\rightarrow$ S $\rightarrow$ W $\rightarrow$ N.
Anti-clockwise movement follows the order N $\rightarrow$ W $\rightarrow$ S $\rightarrow$ E $\rightarrow$ N.
(a) east and make $\frac{1}{2}$ of a revolution clockwise?
Starting direction: East (E)
Turn: $\frac{1}{2}$ revolution clockwise = $180^\circ$ clockwise.
Turning $180^\circ$ clockwise from East:
E $\xrightarrow{90^\circ}$ S $\xrightarrow{90^\circ}$ W
You will face West (W).
(b) east and make $1\frac{1}{2}$ of a revolution clockwise?
Starting direction: East (E)
Turn: $1\frac{1}{2}$ revolutions clockwise = 1 full revolution + $\frac{1}{2}$ revolution clockwise.
One full revolution brings you back to the starting direction (East).
Then, make an additional $\frac{1}{2}$ revolution clockwise from East.
As calculated in part (a), $\frac{1}{2}$ revolution clockwise from East leads to West.
You will face West (W).
(c) west and make $\frac{3}{4}$ of a revolution anti-clockwise?
Starting direction: West (W)
Turn: $\frac{3}{4}$ revolution anti-clockwise = $270^\circ$ anti-clockwise.
Turning $270^\circ$ anti-clockwise from West:
W $\xrightarrow{90^\circ \text{ ACW}}$ S $\xrightarrow{90^\circ \text{ ACW}}$ E $\xrightarrow{90^\circ \text{ ACW}}$ N
(ACW = Anti-Clockwise)
You will face North (N).
(d) south and make one full revolution?
Starting direction: South (S)
Turn: One full revolution = $360^\circ$.
Making a full revolution ($360^\circ$), whether clockwise or anti-clockwise, always brings you back to the starting position/direction.
You will face South (S).
Should we specify clockwise or anti-clockwise for this last question? Why not?
No, we do not need to specify clockwise or anti-clockwise for one full revolution.
Reason: A full revolution means turning $360^\circ$. Regardless of the direction of the turn (clockwise or anti-clockwise), completing a $360^\circ$ turn from any starting direction will always result in facing the original starting direction again.
Question 4. What part of a revolution have you turned through if you stand facing
(a) east and turn clockwise to face north?
(b) south and turn clockwise to face east?
(c) west and turn clockwise to face east?
Answer:
A complete revolution consists of turning through all four directions: North, East, South, West, and back to North. This corresponds to $360^\circ$ or 4 right angles.
Turning from one cardinal direction to the next adjacent direction (e.g., East to South) clockwise represents a $\frac{1}{4}$ turn (1 right angle or $90^\circ$).
(a) east and turn clockwise to face north?
Start facing: East (E)
End facing: North (N)
Turning clockwise from East to North involves passing through South and West:
E $\xrightarrow{\text{clockwise}}$ S (1/4 revolution)
S $\xrightarrow{\text{clockwise}}$ W (1/4 revolution)
W $\xrightarrow{\text{clockwise}}$ N (1/4 revolution)
Total turn = $\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4}$ of a revolution.
You have turned through $\frac{3}{4}$ of a revolution.
(b) south and turn clockwise to face east?
Start facing: South (S)
End facing: East (E)
Turning clockwise from South to East involves passing through West and North:
S $\xrightarrow{\text{clockwise}}$ W (1/4 revolution)
W $\xrightarrow{\text{clockwise}}$ N (1/4 revolution)
N $\xrightarrow{\text{clockwise}}$ E (1/4 revolution)
Total turn = $\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4}$ of a revolution.
You have turned through $\frac{3}{4}$ of a revolution.
(c) west and turn clockwise to face east?
Start facing: West (W)
End facing: East (E)
Turning clockwise from West to East involves passing through North:
W $\xrightarrow{\text{clockwise}}$ N (1/4 revolution)
N $\xrightarrow{\text{clockwise}}$ E (1/4 revolution)
Total turn = $\frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$ of a revolution.
You have turned through $\frac{1}{2}$ of a revolution.
Question 5. Find the number of right angles turned through by the hour hand of a clock when it goes from
(a) 3 to 6
(b) 2 to 8
(c) 5 to 11
(d) 10 to 1
(e) 12 to 9
(f) 12 to 6
Answer:
The hour hand of a clock completes one full revolution ($360^\circ$) in 12 hours.
A right angle is equal to $90^\circ$.
In one full revolution ($360^\circ$), there are $360^\circ / 90^\circ = 4$ right angles.
Since a full revolution takes 12 hours, the number of hours required to turn through one right angle ($90^\circ$) is $12 \text{ hours} / 4 = 3$ hours.
Therefore, we can find the number of right angles turned by dividing the total number of hours moved (clockwise) by 3.
(a) 3 to 6
The hour hand moves clockwise from 3 to 6.
Number of hours moved = $6 - 3 = 3$ hours.
Number of right angles turned = $\frac{\text{Hours moved}}{3} = \frac{3}{3} = 1$.
The hour hand turns through 1 right angle.
(b) 2 to 8
The hour hand moves clockwise from 2 to 8.
Number of hours moved = $8 - 2 = 6$ hours.
Number of right angles turned = $\frac{6}{3} = 2$.
The hour hand turns through 2 right angles.
(c) 5 to 11
The hour hand moves clockwise from 5 to 11.
Number of hours moved = $11 - 5 = 6$ hours.
Number of right angles turned = $\frac{6}{3} = 2$.
The hour hand turns through 2 right angles.
(d) 10 to 1
The hour hand moves clockwise from 10 to 1.
Number of hours moved = (10 to 11) + (11 to 12) + (12 to 1) = $1 + 1 + 1 = 3$ hours.
Number of right angles turned = $\frac{3}{3} = 1$.
The hour hand turns through 1 right angle.
(e) 12 to 9
The hour hand moves clockwise from 12 to 9.
Number of hours moved = 9 hours.
Number of right angles turned = $\frac{9}{3} = 3$.
The hour hand turns through 3 right angles.
(f) 12 to 6
The hour hand moves clockwise from 12 to 6.
Number of hours moved = 6 hours.
Number of right angles turned = $\frac{6}{3} = 2$.
The hour hand turns through 2 right angles.
Question 6. How many right angles do you make if you start facing
(a) south and turn clockwise to west?
(b) north and turn anti-clockwise to east?
(c) west and turn to west?
(d) south and turn to north?
Answer:
A turn of one right angle corresponds to $90^\circ$. Turning between adjacent cardinal directions (North, East, South, West) is a turn of one right angle.
Clockwise direction: N $\rightarrow$ E $\rightarrow$ S $\rightarrow$ W $\rightarrow$ N
Anti-clockwise direction: N $\rightarrow$ W $\rightarrow$ S $\rightarrow$ E $\rightarrow$ N
(a) south and turn clockwise to west?
Starting direction: South (S)
Ending direction: West (W)
Direction of turn: Clockwise
Following the clockwise path from South to West: S $\rightarrow$ W.
This is a single step between adjacent directions in the clockwise sequence.
Therefore, you make 1 right angle.
(b) north and turn anti-clockwise to east?
Starting direction: North (N)
Ending direction: East (E)
Direction of turn: Anti-clockwise
Following the anti-clockwise path from North to East:
N $\xrightarrow{\text{ACW}}$ W (1 right angle)
W $\xrightarrow{\text{ACW}}$ S (1 right angle)
S $\xrightarrow{\text{ACW}}$ E (1 right angle)
(ACW = Anti-Clockwise)
Total turn = $1 + 1 + 1 = 3$ right angles.
Therefore, you make 3 right angles.
(c) west and turn to west?
Starting direction: West (W)
Ending direction: West (W)
Turning from a direction back to the same direction implies either no turn or a full revolution.
If there is no actual turn, the number of right angles is 0.
If you make a complete revolution (turning $360^\circ$) to end up facing West again, you turn through 4 right angles ($360^\circ / 90^\circ = 4$).
Assuming the question implies completing a full turn:
Therefore, you make 4 right angles.
(d) south and turn to north?
Starting direction: South (S)
Ending direction: North (N)
North is directly opposite South. Turning from South to North is a half revolution ($180^\circ$).
The number of right angles in a $180^\circ$ turn is $180^\circ / 90^\circ = 2$.
This is true whether you turn clockwise (S $\rightarrow$ W $\rightarrow$ N) or anti-clockwise (S $\rightarrow$ E $\rightarrow$ N).
Therefore, you make 2 right angles.
Question 7. Where will the hour hand of a clock stop if it starts
(a) from 6 and turns through 1 right angle?
(b) from 8 and turns through 2 right angles?
(c) from 10 and turns through 3 right angles?
(d) from 7 and turns through 2 straight angles?
Answer:
We need to determine the stopping position of the hour hand after specific turns. We assume the turns are clockwise.
Key information:
- One full revolution (12 hours) is $360^\circ$.
- One right angle is $90^\circ$. The hour hand turns $90^\circ$ in $12 / (360/90) = 12 / 4 = 3$ hours.
- One straight angle is $180^\circ$. The hour hand turns $180^\circ$ in $12 / (360/180) = 12 / 2 = 6$ hours.
(a) from 6 and turns through 1 right angle?
Starting position: 6
Turn: 1 right angle = 3 hours clockwise.
Calculation: Moving 3 hours clockwise from 6 means $6 + 3 = 9$.
The hour hand will stop at 9.
(b) from 8 and turns through 2 right angles?
Starting position: 8
Turn: 2 right angles = $2 \times 3 = 6$ hours clockwise.
Calculation: Moving 6 hours clockwise from 8 means $8 + 6 = 14$. On a 12-hour clock, 14 corresponds to 2 (after 12, we have 1, then 2).
The hour hand will stop at 2.
(c) from 10 and turns through 3 right angles?
Starting position: 10
Turn: 3 right angles = $3 \times 3 = 9$ hours clockwise.
Calculation: Moving 9 hours clockwise from 10 means $10 + 9 = 19$. On a 12-hour clock, 19 corresponds to 7 (after 12, count 7 more hours: 1, 2, 3, 4, 5, 6, 7).
The hour hand will stop at 7.
(d) from 7 and turns through 2 straight angles?
Starting position: 7
Turn: 2 straight angles. One straight angle is $180^\circ$ or 6 hours.
Total turn = $2 \times 6 = 12$ hours clockwise.
A turn of 12 hours is exactly one full revolution ($360^\circ$).
Calculation: Moving 12 hours clockwise from 7 brings the hand back to its starting position.
The hour hand will stop at 7.
Exercise 5.3
Question 1. Match the following :
(i) Straight angle
(ii) Right angle
(iii) Acute angle
(iv) Obtuse angle
(v) Reflex angle
(a) Less than one-fourth of a revolution
(b) More than half a revolution
(c) Half of a revolution
(d) One-fourth of a revolution
(e) Between $\frac{1}{4}$ and $\frac{1}{2}$ of a revolution
(f) One complete revolution
Answer:
First, let's understand the relationship between angles and revolutions:
One complete revolution is $360^\circ$.
$\frac{1}{4}$ of a revolution is $\frac{1}{4} \times 360^\circ = 90^\circ$. This is a Right angle.
$\frac{1}{2}$ of a revolution is $\frac{1}{2} \times 360^\circ = 180^\circ$. This is a Straight angle.
Less than $\frac{1}{4}$ of a revolution means less than $90^\circ$. This describes an Acute angle.
Between $\frac{1}{4}$ and $\frac{1}{2}$ of a revolution means between $90^\circ$ and $180^\circ$. This describes an Obtuse angle.
More than $\frac{1}{2}$ of a revolution means more than $180^\circ$. This describes a Reflex angle.
Now we can match the items:
(i) Straight angle: Corresponds to exactly $180^\circ$, which is half of a revolution.
Match: (i) $\leftrightarrow$ (c) Half of a revolution
(ii) Right angle: Corresponds to exactly $90^\circ$, which is one-fourth of a revolution.
Match: (ii) $\leftrightarrow$ (d) One-fourth of a revolution
(iii) Acute angle: Corresponds to less than $90^\circ$, which is less than one-fourth of a revolution.
Match: (iii) $\leftrightarrow$ (a) Less than one-fourth of a revolution
(iv) Obtuse angle: Corresponds to between $90^\circ$ and $180^\circ$, which is between $\frac{1}{4}$ and $\frac{1}{2}$ of a revolution.
Match: (iv) $\leftrightarrow$ (e) Between $\frac{1}{4}$ and $\frac{1}{2}$ of a revolution
(v) Reflex angle: Corresponds to more than $180^\circ$, which is more than half a revolution.
Match: (v) $\leftrightarrow$ (b) More than half a revolution
Final Matches:
(i) $\rightarrow$ (c)
(ii) $\rightarrow$ (d)
(iii) $\rightarrow$ (a)
(iv) $\rightarrow$ (e)
(v) $\rightarrow$ (b)
(Note: Option (f) 'One complete revolution' corresponds to $360^\circ$, which is not listed as an option on the left side.)
Question 2. Classify each one of the following angles as right, straight, acute, obtuse or reflex:
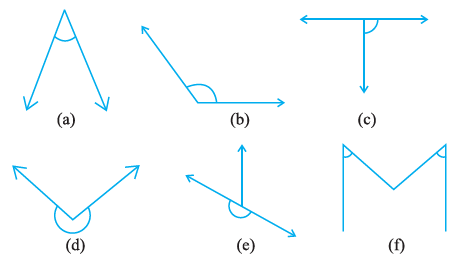
Answer:
We classify each angle based on its measure compared to $90^\circ$ (right angle) and $180^\circ$ (straight angle).
(a)
The angle shown is less than $90^\circ$.
Therefore, it is an Acute angle.
(b)
The angle shown is greater than $90^\circ$ but less than $180^\circ$.
Therefore, it is an Obtuse angle.
(c)
The angle shown is exactly $90^\circ$ (indicated by the square symbol).
Therefore, it is a Right angle.
(d)
The angle shown (indicated by the arc) is greater than $180^\circ$.
Therefore, it is a Reflex angle.
(e)
The angle shown forms a straight line, which is exactly $180^\circ$.
Therefore, it is a Straight angle.
(f)
Both angles shown are less than $90^\circ$.
Therefore, both are Acute angles.
Exercise 5.4
Question 1. What is the measure of
(i) a right angle?
(ii) a straight angle?
Answer:
(i) a right angle?
A right angle is an angle that corresponds to one-quarter of a full revolution or rotation. It is formed by two perpendicular lines.
The measure of a right angle is $90^\circ$.
(ii) a straight angle?
A straight angle is an angle that corresponds to one-half of a full revolution or rotation. It forms a straight line.
The measure of a straight angle is $180^\circ$. It is equivalent to two right angles ($2 \times 90^\circ = 180^\circ$).
Question 2. Say True or False :
(a) The measure of an acute angle < 90°.
(b) The measure of an obtuse angle < 90°.
(c) The measure of a reflex angle > 180°.
(d) The measure of one complete revolution = 360°.
(e) If m∠A = 53° and m∠B = 35°, then m∠A > m∠B .
Answer:
(a) The measure of an acute angle < 90°.
An acute angle is defined as an angle whose measure is greater than $0^\circ$ and less than $90^\circ$. Therefore, its measure is always less than $90^\circ$.
The statement is True.
(b) The measure of an obtuse angle < 90°.
An obtuse angle is defined as an angle whose measure is greater than $90^\circ$ and less than $180^\circ$. Therefore, its measure is always greater than $90^\circ$, not less.
The statement is False.
(c) The measure of a reflex angle > 180°.
A reflex angle is defined as an angle whose measure is greater than $180^\circ$ and less than $360^\circ$. Therefore, its measure is always greater than $180^\circ$.
The statement is True.
(d) The measure of one complete revolution = 360°.
One complete revolution corresponds to turning in a full circle, which is defined as $360^\circ$.
The statement is True.
(e) If m∠A = 53° and m∠B = 35°, then m∠A > m∠B.
We are given $m\angle A = 53^\circ$ and $m\angle B = 35^\circ$.
Comparing the numerical values, we see that $53 > 35$.
Therefore, $m\angle A > m\angle B$.
The statement is True.
Question 3. Write down the measures of
(a) some acute angles.
(b) some obtuse angles.
(give at least two examples of each).
Answer:
(a) Some acute angles.
An acute angle is an angle whose measure is greater than $0^\circ$ and less than $90^\circ$.
Examples of acute angles:
1. $35^\circ$
2. $70^\circ$
(Other examples could include $20^\circ$, $45^\circ$, $89^\circ$, etc.)
(b) Some obtuse angles.
An obtuse angle is an angle whose measure is greater than $90^\circ$ and less than $180^\circ$.
Examples of obtuse angles:
1. $110^\circ$
2. $160^\circ$
(Other examples could include $95^\circ$, $135^\circ$, $175^\circ$, etc.)
Question 4. Measure the angles given below using the Protractor and write down the measure.


Answer:
To measure the angles, place the center of the protractor at the vertex of the angle and align the base line of the protractor with one arm of the angle. Read the measure on the protractor where the other arm crosses the scale.
Assuming the angles are measured using a protractor, the approximate measures are:
(a)
The measure of the angle is approximately $45^\circ$.
(This is an acute angle.)
(b)
The measure of the angle is approximately $120^\circ$.
(This is an obtuse angle.)
(c)
The measure of the angle is exactly $90^\circ$.
(This is a right angle.)
(d)
This figure shows three angles. Measuring each from left to right:
1. The first angle (left) measures approximately $60^\circ$. (Acute angle)
2. The second angle (right) measures approximately $90^\circ$. (Right angle)
3. The third angle (middle) measures approximately $130^\circ$. (Obtuse angle)
(Note: Precise measurements might vary slightly depending on the drawing and the accuracy of the protractor used.)
Question 5. Which angle has a large measure?
First estimate and then measure.
Measure of Angle A =
Measure of Angle B =
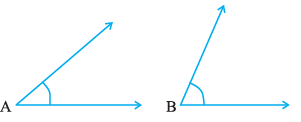
Answer:
Estimation:
By visually inspecting the two angles, Angle B appears to have a wider opening compared to Angle A.
Therefore, the initial estimate is that Angle B has a larger measure than Angle A.
Measurement:
Using a protractor to measure the angles:
Measure of Angle A $\approx$ $40^\circ$
Measure of Angle B $\approx$ $65^\circ$
(Note: These are approximate values obtained by measuring the image.)
Comparison and Conclusion:
Comparing the measured values:
$65^\circ > 40^\circ$
This means that the measure of Angle B is greater than the measure of Angle A.
Therefore, Angle B has a larger measure.
Question 6. From these two angles which has larger measure? Estimate and then confirm by measuring them.
.png)
Answer:
1. Estimation
Let's refer to the angle on the left as Angle A and the angle on the right as Angle B.
By visual inspection, the opening between the arms of Angle B appears to be wider than the opening between the arms of Angle A. Therefore, it is estimated that Angle B has a larger measure.
2. Confirmation by Measurement
To confirm this estimation, we measure both angles using a protractor.
The steps to measure are:
1. Place the center point of the protractor on the vertex of the angle.
2. Align the baseline of the protractor with one arm of the angle.
3. Read the degree mark on the protractor where the second arm crosses the scale.
Upon measuring the two angles, we get the following approximate values:
Measure of Angle A $\approx 45^\circ$.
Measure of Angle B $\approx 60^\circ$.
3. Conclusion
By comparing the measured values, we can see that $60^\circ > 45^\circ$.
This confirms our initial estimation. Therefore, the second angle (Angle B) has a larger measure than the first angle (Angle A).
Question 7. Fill in the blanks with acute, obtuse, right or straight :
(a) An angle whose measure is less than that of a right angle is______.
(b) An angle whose measure is greater than that of a right angle is ______.
(c) An angle whose measure is the sum of the measures of two right angles is _____.
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is ______.
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be _______.
Answer:
(a) An angle whose measure is less than that of a right angle ($90^\circ$) is acute.
Reason: Acute angles are defined as angles measuring between $0^\circ$ and $90^\circ$.
(b) An angle whose measure is greater than that of a right angle ($90^\circ$) is obtuse (assuming it is less than a straight angle, $180^\circ$).
Reason: Obtuse angles are defined as angles measuring between $90^\circ$ and $180^\circ$. If the angle could be greater than $180^\circ$, it could also be reflex. However, "obtuse" is the classification for angles just larger than right angles but less than straight angles.
(c) An angle whose measure is the sum of the measures of two right angles is straight.
Reason: A right angle measures $90^\circ$. The sum of two right angles is $90^\circ + 90^\circ = 180^\circ$. An angle measuring $180^\circ$ is called a straight angle.
(d) When the sum of the measures of two angles is that of a right angle ($90^\circ$), then each one of them is acute.
Reason: Let the two angles be $x$ and $y$. We have $x + y = 90^\circ$. Since angle measures must be positive, both $x > 0^\circ$ and $y > 0^\circ$. This implies $x < 90^\circ$ and $y < 90^\circ$. Angles greater than $0^\circ$ and less than $90^\circ$ are acute angles.
(e) When the sum of the measures of two angles is that of a straight angle ($180^\circ$) and if one of them is acute then the other should be obtuse.
Reason: Let the two angles be $x$ and $y$. We have $x + y = 180^\circ$. Let $x$ be the acute angle, so $0^\circ < x < 90^\circ$. Then $y = 180^\circ - x$. Subtracting the inequality $0^\circ < x < 90^\circ$ from $180^\circ$ (and reversing the inequality signs): $180^\circ - 90^\circ < 180^\circ - x < 180^\circ - 0^\circ$, which means $90^\circ < y < 180^\circ$. An angle between $90^\circ$ and $180^\circ$ is an obtuse angle.
Question 8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor).
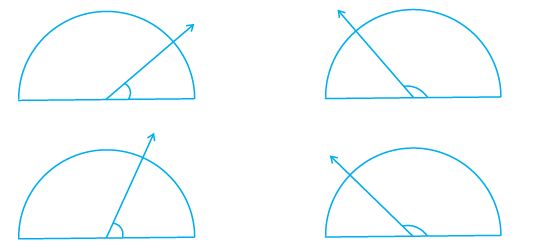
Answer:
We will first visually estimate the measure of each angle and then measure it using a protractor.
Figure 1 (Top Left):
Estimation: The angle appears to be acute, less than $90^\circ$ and also less than $45^\circ$. My estimate is around $35^\circ - 40^\circ$.
Measurement: Using a protractor, the measure is approximately $40^\circ$.
Figure 2 (Top Right):
Estimation: The angle appears to be obtuse, greater than $90^\circ$ but less than $180^\circ$. It looks significantly wider than $90^\circ$. My estimate is around $125^\circ - 135^\circ$.
Measurement: Using a protractor, the measure is approximately $130^\circ$.
Figure 3 (Bottom Left):
Estimation: The angle appears to be acute, less than $90^\circ$. It looks wider than $45^\circ$. My estimate is around $60^\circ - 70^\circ$.
Measurement: Using a protractor, the measure is approximately $65^\circ$.
Figure 4 (Bottom Right):
Estimation: The angle appears to be obtuse, greater than $90^\circ$. It looks similar to, perhaps slightly larger than, the angle in Figure 2. My estimate is around $130^\circ - 140^\circ$.
Measurement: Using a protractor, the measure is approximately $135^\circ$.
(Note: The measured values are approximations based on the provided image.)
Question 9. Find the angle measure between the hands of the clock in each figure :
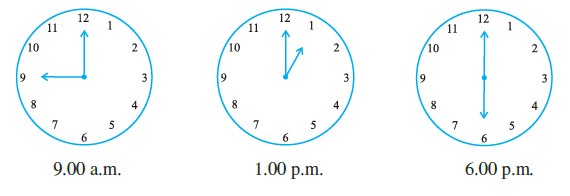
Answer:
To find the angle between the hands of a clock, we can use the fact that a clock face represents a full circle of $360^\circ$.
There are 12 hour markings on the clock. The angle between any two consecutive hour markings is $\frac{360^\circ}{12} = 30^\circ$.
Figure 1 (Time: 9:00):
The minute hand points at 12.
The hour hand points at 9.
The number of hour intervals between 9 and 12 (moving clockwise from 9) is 3 (from 9 to 10, 10 to 11, 11 to 12).
The angle between the hands = (Number of intervals) $\times$ (Angle per interval)
Angle = $3 \times 30^\circ = 90^\circ$.
The angle measure is $90^\circ$ (a right angle).
Figure 2 (Time: 1:00):
The minute hand points at 12.
The hour hand points at 1.
The number of hour intervals between 12 and 1 is 1.
Angle = $1 \times 30^\circ = 30^\circ$.
The angle measure is $30^\circ$ (an acute angle).
Figure 3 (Time: 6:00):
The minute hand points at 12.
The hour hand points at 6.
The number of hour intervals between 6 and 12 is 6.
Angle = $6 \times 30^\circ = 180^\circ$.
The angle measure is $180^\circ$ (a straight angle).
Question 10. Investigate
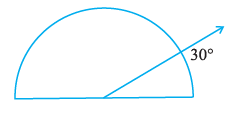
In the given figure, the angle measures 30°. Look at the same figure through a magnifying glass.
Does the angle becomes larger? Does the size of the angle change?
Answer:
The measure of the angle shown in the figure is given as $30^\circ$.
When we look at the figure through a magnifying glass, the entire figure, including the lines forming the angle, will appear larger visually.
However, a magnifying glass only changes the apparent size of the object being viewed; it does not alter the object's actual properties or geometric relationships.
The measure of an angle refers to the amount of turn or rotation between its two arms. This property is independent of how large or small the arms are drawn or how much they are magnified.
Does the angle become larger?
The visual representation of the angle (the drawing itself) will appear larger, but the measure of the angle ($30^\circ$) does not become larger.
Does the size of the angle change?
No, the size (or measure) of the angle does not change. It remains $30^\circ$ even when viewed through a magnifying glass.
The measure of an angle is an intrinsic property and is not affected by magnification.
Question 11. Measure and classify each angle:
.png)
| Angle | Measure | Type |
|---|---|---|
| $\angle$ AOB | ||
| $\angle$ AOC | ||
| $\angle$ BOC | ||
| $\angle$ DOC | ||
| $\angle$ DOA | ||
| $\angle$ DOB |
Answer:
To find the measure and type of each angle, we use a protractor placed with its center at vertex O and its base line along OA.
By measuring the angles from the figure:
| Angle | Measure (Approx.) | Type |
| $\angle$ AOB | $40^\circ$ | Acute |
| $\angle$ AOC | $125^\circ$ | Obtuse |
| $\angle$ BOC | $85^\circ$ (Calculated as $\angle AOC - \angle AOB = 125^\circ - 40^\circ$) | Acute |
| $\angle$ DOC | $95^\circ$ (Calculated as $\angle DOB - \angle BOC = 180^\circ - 85^\circ$, assuming B, O, D are collinear) | Obtuse |
| $\angle$ DOA | $140^\circ$ (Calculated as $\angle DOB - \angle AOB = 180^\circ - 40^\circ$, assuming B, O, D are collinear) | Obtuse |
| $\angle$ DOB | $180^\circ$ (Visually appears to be a straight line) | Straight |
Note: Measurements are approximate and based on visual inspection and common values associated with this textbook figure. The calculation for some angles assumes that points B, O, and D lie on a straight line, as visually suggested by the figure making $\angle DOB$ a straight angle.
Exercise 5.5
Question 1. Which of the following are models for perpendicular lines :
(a) The adjacent edges of a table top.
(b) The lines of a railway track.
(c) The line segments forming the letter ‘L’.
(d) The letter V.
Answer:
Perpendicular lines are lines that intersect each other at a right angle ($90^\circ$). Let's analyze each option:
(a) The adjacent edges of a table top.
Table tops are generally rectangular in shape. The adjacent edges of a rectangle meet at a corner, forming a $90^\circ$ angle. Therefore, the adjacent edges of a table top are a model for perpendicular lines.
(b) The lines of a railway track.
Railway tracks are designed to be parallel. Parallel lines never intersect. Therefore, the lines of a railway track are not a model for perpendicular lines; they are a model for parallel lines.
(c) The line segments forming the letter ‘L’.
The letter 'L' is typically formed by one vertical line segment and one horizontal line segment meeting at an endpoint. These segments form a $90^\circ$ angle. Therefore, the line segments forming the letter 'L' are a model for perpendicular lines.
(d) The letter V.
The letter 'V' is formed by two line segments meeting at a point. The angle between these segments is typically acute (less than $90^\circ$). It is not a right angle. Therefore, the letter 'V' is not a model for perpendicular lines.
Conclusion:
The models for perpendicular lines among the given options are (a) The adjacent edges of a table top and (c) The line segments forming the letter ‘L’.
Question 2. Let $\overline{PQ}$ be the perpendicular to the line segment $\overline{XY}$ . Let $\overline{PQ}$ and $\overline{XY}$ intersect in the point A. What is the measure of ∠PAY ?
Answer:
Given:
Line segment $\overline{PQ}$ is perpendicular to the line segment $\overline{XY}$.
The notation for this is $\overline{PQ} \perp \overline{XY}$.
The line segments $\overline{PQ}$ and $\overline{XY}$ intersect at point A.
To Find:
The measure of the angle $\angle PAY$.
Solution:
By definition, when two lines or line segments are perpendicular, they intersect each other at a right angle.
A right angle has a measure of exactly $90^\circ$.
We are given that $\overline{PQ} \perp \overline{XY}$ and they intersect at point A.
This means that all angles formed at the intersection point A are right angles.
The angle $\angle PAY$ is one of the angles formed by the intersection of $\overline{PQ}$ and $\overline{XY}$ at point A.
Therefore, the measure of $\angle PAY$ must be $90^\circ$.
$m\angle PAY = 90^\circ$.
Question 3. There are two set-squares in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
Answer:
A standard geometry box contains two types of set-squares, which are triangular rulers used for drawing specific angles.
Set-Square 1: The 45-45-90 Set-Square
This set-square has the shape of a right-angled isosceles triangle.
The measures of the angles formed at its corners are: $45^\circ$, $45^\circ$, and $90^\circ$.
Set-Square 2: The 30-60-90 Set-Square
This set-square has the shape of a right-angled scalene triangle.
The measures of the angles formed at its corners are: $30^\circ$, $60^\circ$, and $90^\circ$.
Common Angle Measure
To find the common angle measure, we compare the sets of angles for both set-squares:
Angles of Set-Square 1: {$45^\circ$, $45^\circ$, $90^\circ$}
Angles of Set-Square 2: {$30^\circ$, $60^\circ$, $90^\circ$}
Yes, they have an angle measure in common. The common angle is $90^\circ$ (the right angle).
Question 4. Study the diagram. The line l is perpendicular to line m
(a) Is CE = EG?
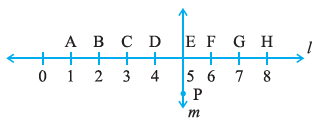
(b) Does PE bisect CG?
(c) Identify any two line segments for which PE is the perpendicular bisector.
(d) Are these true?
(i) AC > FG
(ii) CD = GH
(iii) BC < EH.
Answer:
From the diagram, we can observe that points A, B, C, D, E, F, G, H are marked on line $m$ at equal intervals. Let's assume the distance between consecutive points is 1 unit.
We can assign positions to the points, starting with A=0: A=0, B=1, C=2, D=3, E=4, F=5, G=6, H=7.
Line $l$ is perpendicular to line $m$ ($l \perp m$) and they intersect at point E.
(a) Is CE = EG?
To check if $CE = EG$, we need to find the lengths of these segments.
Length $CE = (\text{Position of E}) - (\text{Position of C}) = 4 - 2 = 2$ units.
Length $EG = (\text{Position of G}) - (\text{Position of E}) = 6 - 4 = 2$ units.
Since both lengths are equal to 2 units:
Yes, $CE = EG$.
(b) Does PE bisect CG?
The line segment $\overline{PE}$ (which lies on line $l$) intersects the line segment $\overline{CG}$ at point E.
For $\overline{PE}$ to bisect $\overline{CG}$, the point E must be the midpoint of $\overline{CG}$.
A point is the midpoint of a segment if it divides the segment into two equal parts.
From part (a), we found that $CE = EG$.
Since E lies on $\overline{CG}$ and $CE = EG$, E is the midpoint of $\overline{CG}$.
Therefore, Yes, $\overline{PE}$ bisects $\overline{CG}$.
(c) Identify any two line segments for which PE is the perpendicular bisector.
For $\overline{PE}$ to be the perpendicular bisector of a line segment, two conditions must be met:
1. $\overline{PE}$ must be perpendicular to the line segment.
2. $\overline{PE}$ must intersect the line segment at its midpoint.
We are given that line $l$ (containing PE) is perpendicular to line $m$. So, $\overline{PE}$ is perpendicular to any segment lying on line $m$. We need to find segments on line $m$ for which E (the intersection point) is the midpoint.
Segment 1: From part (b), we know E is the midpoint of $\overline{CG}$. Since $\overline{PE} \perp \overline{CG}$ and E is the midpoint, $\overline{PE}$ is the perpendicular bisector of $\overline{CG}$.
Segment 2: Consider the segment $\overline{DF}$. Position D=3, Position F=5. Midpoint position = $(3+5)/2 = 4$. Point E is at position 4. Length $DE = 4-3=1$ unit. Length $EF = 5-4=1$ unit. Since $DE=EF$, E is the midpoint of $\overline{DF}$. Since $\overline{PE} \perp \overline{DF}$, $\overline{PE}$ is the perpendicular bisector of $\overline{DF}$.
(Another possible answer: Consider $\overline{BH}$. Position B=1, Position H=7. Midpoint position = $(1+7)/2 = 4$. E is the midpoint of $\overline{BH}$. So $\overline{PE}$ is the perpendicular bisector of $\overline{BH}$.)
Two such line segments are $\overline{CG}$ and $\overline{DF}$.
(d) Are these true?
(i) AC > FG
Length $AC = (\text{Position of C}) - (\text{Position of A}) = 2 - 0 = 2$ units.
Length $FG = (\text{Position of G}) - (\text{Position of F}) = 6 - 5 = 1$ unit.
Is $2 > 1$? Yes.
Therefore, the statement $AC > FG$ is True.
(ii) CD = GH
Length $CD = (\text{Position of D}) - (\text{Position of C}) = 3 - 2 = 1$ unit.
Length $GH = (\text{Position of H}) - (\text{Position of G}) = 7 - 6 = 1$ unit.
Is $1 = 1$? Yes.
Therefore, the statement $CD = GH$ is True.
(iii) BC < EH
Length $BC = (\text{Position of C}) - (\text{Position of B}) = 2 - 1 = 1$ unit.
Length $EH = (\text{Position of H}) - (\text{Position of E}) = 7 - 4 = 3$ units.
Is $1 < 3$? Yes.
Therefore, the statement $BC < EH$ is True.
Exercise 5.6
Question 1. Name the types of following triangles :
(a) Triangle with lengths of sides 7 cm, 8 cm and 9 cm.
(b) ∆ABC with AB = 8.7 cm, AC = 7 cm and BC = 6 cm.
(c) ∆PQR such that PQ = QR = PR = 5 cm.
(d) ∆DEF with m∠D = 90°
(e) ∆XYZ with m∠Y = 90° and XY = YZ.
(f) ∆LMN with m∠L = 30°, m∠M = 70° and m∠N = 80°
Answer:
Triangles can be classified based on their side lengths or their angle measures.
(a) Triangle with lengths of sides 7 cm, 8 cm and 9 cm.
Analysis: The lengths of the sides are 7 cm, 8 cm, and 9 cm. Since all three sides have different lengths, the triangle is classified based on its sides.
Type: Scalene triangle.
(b) ∆ABC with AB = 8.7 cm, AC = 7 cm and BC = 6 cm.
Analysis: The lengths of the sides are 8.7 cm, 7 cm, and 6 cm. All three sides have different lengths.
Type: Scalene triangle.
(c) ∆PQR such that PQ = QR = PR = 5 cm.
Analysis: The lengths of all three sides are equal (5 cm). A triangle with all sides equal is classified based on its sides.
Type: Equilateral triangle.
Note: An equilateral triangle is also always an acute-angled triangle, as all its angles are $60^\circ$.
(d) ∆DEF with m∠D = 90°
Analysis: One of the angles ($\angle D$) measures $90^\circ$. A triangle containing a right angle is classified based on its angles.
Type: Right-angled triangle.
(e) ∆XYZ with m∠Y = 90° and XY = YZ.
Analysis: The triangle has one angle equal to $90^\circ$ (m∠Y), making it a right-angled triangle. Also, two of its sides (XY and YZ) are equal in length, making it an isosceles triangle.
Type: Isosceles right-angled triangle (classified by both angles and sides).
(f) ∆LMN with m∠L = 30°, m∠M = 70° and m∠N = 80°
Analysis: All three angles ($30^\circ$, $70^\circ$, $80^\circ$) are less than $90^\circ$. A triangle where all angles are acute is classified based on its angles.
Type: Acute-angled triangle.
Note: Since all angles are different, the sides opposite to these angles will also be different. Therefore, it is also a scalene triangle.
Question 2. Match the following :
Measures of Triangle
(i) 3 sides of equal length
(ii) 2 sides of equal length
(iii) All sides are of different length
(iv) 3 acute angles
(v) 1 right angle
(vi) 1 obtuse angle
(vii) 1 right angle with two sides of equal length
Type of Triangle
(a) Scalene
(b) Isosceles right angled
(c) Obtuse angled
(d) Right angled
(e) Equilateral
(f) Acute angled
(g) Isosceles
Answer:
Here are the matches between the measures of the triangle and its type:
(i) 3 sides of equal length
A triangle with 3 sides of equal length is called an Equilateral triangle.
Match: (i) $\leftrightarrow$ (e)
(ii) 2 sides of equal length
A triangle with 2 sides of equal length is called an Isosceles triangle.
Match: (ii) $\leftrightarrow$ (g)
(iii) All sides are of different length
A triangle with all sides of different length is called a Scalene triangle.
Match: (iii) $\leftrightarrow$ (a)
(iv) 3 acute angles
A triangle with 3 acute angles (all angles less than $90^\circ$) is called an Acute angled triangle.
Match: (iv) $\leftrightarrow$ (f)
(v) 1 right angle
A triangle with 1 right angle ($90^\circ$) is called a Right angled triangle.
Match: (v) $\leftrightarrow$ (d)
(vi) 1 obtuse angle
A triangle with 1 obtuse angle (one angle greater than $90^\circ$ and less than $180^\circ$) is called an Obtuse angled triangle.
Match: (vi) $\leftrightarrow$ (c)
(vii) 1 right angle with two sides of equal length
A triangle with 1 right angle and two sides of equal length (specifically, the two sides forming the right angle) is called an Isosceles right angled triangle.
Match: (vii) $\leftrightarrow$ (b)
Question 3. Name each of the following triangles in two different ways: (you may judge the nature of the angle by observation)
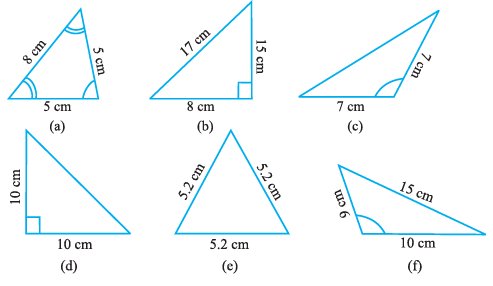
Answer:
We need to classify each triangle based on both its side lengths and its angle measures.
(a)
Based on sides: Two sides have equal length (5 cm). This is an Isosceles triangle.
Based on angles: All angles appear to be less than $90^\circ$. This is an Acute-angled triangle.
Combined classification: Acute-angled Isosceles triangle.
(b)
Based on sides: All sides have different lengths (8 cm, 15 cm, 17 cm). This is a Scalene triangle.
Based on angles: One angle appears to be exactly $90^\circ$ (It's a Pythagorean triple: $8^2 + 15^2 = 64 + 225 = 289 = 17^2$). This is a Right-angled triangle.
Combined classification: Right-angled Scalene triangle.
(c)
Based on sides: Two sides have equal length (7 cm). This is an Isosceles triangle.
Based on angles: One angle appears to be greater than $90^\circ$. This is an Obtuse-angled triangle.
Combined classification: Obtuse-angled Isosceles triangle.
(d)
Based on sides: Two sides have equal length (10 cm). This is an Isosceles triangle.
Based on angles: One angle is marked as $90^\circ$. This is a Right-angled triangle.
Combined classification: Right-angled Isosceles triangle.
(e)
Based on sides: All three sides have equal length (5.2 cm). This is an Equilateral triangle.
Based on angles: All angles in an equilateral triangle are $60^\circ$, which are less than $90^\circ$. This is an Acute-angled triangle.
Combined classification: Acute-angled Equilateral triangle.
(f)
Based on sides: All sides have different lengths (9 cm, 10 cm, 15 cm). This is a Scalene triangle.
Based on angles: One angle appears to be greater than $90^\circ$. This is an Obtuse-angled triangle.
Combined classification: Obtuse-angled Scalene triangle.
Question 4. Try to construct triangles using match sticks. Some are shown here.
Can you make a triangle with
(a) 3 matchsticks?
(b) 4 matchsticks?
(c) 5 matchsticks?
(d) 6 matchsticks?
(Remember you have to use all the available matchsticks in each case)
Name the type of triangle in each case.
If you cannot make a triangle, think of reasons for it.
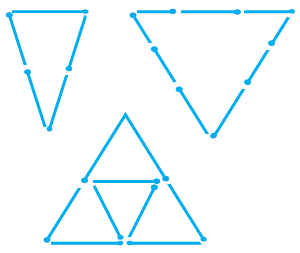
Answer:
To form a triangle with given side lengths (represented by the number of matchsticks), the Triangle Inequality Theorem must be satisfied: The sum of the lengths of any two sides must be greater than the length of the third side.
Let the length of one matchstick be 1 unit.
(a) 3 matchsticks?
We need to form a triangle with a total perimeter of 3 units, using 3 matchsticks.
The only possible combination of side lengths is 1 unit, 1 unit, 1 unit.
Checking the Triangle Inequality:
$1 + 1 = 2 > 1$ (True)
Since the condition is satisfied, Yes, a triangle can be formed.
Type of Triangle: Since all three sides are equal (1, 1, 1), it is an Equilateral triangle.
(b) 4 matchsticks?
We need to form a triangle with a total perimeter of 4 units, using 4 matchsticks.
Possible combinations of integer side lengths adding to 4:
1 unit, 1 unit, 2 units.
Checking the Triangle Inequality:
$1 + 1 = 2$. Is $2 > 2$? No, it is not.
Since the sum of the two shorter sides is not greater than the longest side, No, a triangle cannot be formed.
Reason: The sum of the lengths of the two smaller sides (1+1) is equal to the length of the third side (2). The matchsticks would form a straight line segment of length 2 with the third matchstick lying on top.
(c) 5 matchsticks?
We need to form a triangle with a total perimeter of 5 units, using 5 matchsticks.
Possible combinations of integer side lengths adding to 5:
- 1 unit, 1 unit, 3 units: Check $1 + 1 > 3$? (False, $2 \ngtr 3$). Cannot form.
- 1 unit, 2 units, 2 units: Check:
$1 + 2 = 3 > 2$ (True)
$2 + 2 = 4 > 1$ (True)
Since the conditions are satisfied for (1, 2, 2), Yes, a triangle can be formed.
Type of Triangle: Since two sides are equal (2 units, 2 units), it is an Isosceles triangle.
(d) 6 matchsticks?
We need to form a triangle with a total perimeter of 6 units, using 6 matchsticks.
Possible combinations of integer side lengths adding to 6:
- 1 unit, 1 unit, 4 units: Check $1 + 1 > 4$? (False, $2 \ngtr 4$). Cannot form.
- 1 unit, 2 units, 3 units: Check $1 + 2 > 3$? (False, $3 \ngtr 3$). Cannot form.
- 2 units, 2 units, 2 units: Check:
$2 + 2 = 4 > 2$ (True)
Since the conditions are satisfied for (2, 2, 2), Yes, a triangle can be formed.
Type of Triangle: Since all three sides are equal (2, 2, 2), it is an Equilateral triangle.
Exercise 5.7
Question 1. Say True or False :
(a) Each angle of a rectangle is a right angle.
(b) The opposite sides of a rectangle are equal in length.
(c) The diagonals of a square are perpendicular to one another.
(d) All the sides of a rhombus are of equal length.
(e) All the sides of a parallelogram are of equal length.
(f) The opposite sides of a trapezium are parallel.
Answer:
(a) Each angle of a rectangle is a right angle.
By definition, a rectangle is a quadrilateral with four right angles ($90^\circ$).
The statement is True.
(b) The opposite sides of a rectangle are equal in length.
This is a fundamental property of a rectangle. Opposite sides are always equal.
The statement is True.
(c) The diagonals of a square are perpendicular to one another.
A square is a special type of rhombus (and rectangle). A property of rhombuses is that their diagonals intersect at right angles ($90^\circ$), meaning they are perpendicular.
The statement is True.
(d) All the sides of a rhombus are of equal length.
By definition, a rhombus is a quadrilateral with all four sides having equal length.
The statement is True.
(e) All the sides of a parallelogram are of equal length.
A parallelogram has opposite sides equal in length, but adjacent sides are not necessarily equal. Only special parallelograms like rhombuses and squares have all sides equal.
The statement is False.
(f) The opposite sides of a trapezium are parallel.
A trapezium (or trapezoid) is defined as a quadrilateral with at least one pair of opposite sides parallel. It does not require both pairs of opposite sides to be parallel (if both pairs were parallel, it would be a parallelogram).
The statement is False (as it implies both pairs of opposite sides are parallel, which is not the definition of a general trapezium).
Question 2. Give reasons for the following :
(a) A square can be thought of as a special rectangle.
(b) A rectangle can be thought of as a special parallelogram.
(c) A square can be thought of as a special rhombus.
(d) Squares, rectangles, parallelograms are all quadrilaterals.
(e) Square is also a parallelogram.
Answer:
(a) A square can be thought of as a special rectangle.
Reason: A rectangle is defined as a parallelogram with four right angles. A square has four right angles and also has all four sides equal. Since a square satisfies the property of having four right angles, it fulfills the basic requirement of a rectangle. The additional property of having all sides equal makes it a 'special' case of a rectangle.
(b) A rectangle can be thought of as a special parallelogram.
Reason: A parallelogram is defined as a quadrilateral with opposite sides parallel and equal in length. A rectangle satisfies this condition (its opposite sides are parallel and equal). The additional property of a rectangle is that all its angles are right angles ($90^\circ$). This specific angle requirement makes the rectangle a 'special' type of parallelogram.
(c) A square can be thought of as a special rhombus.
Reason: A rhombus is defined as a parallelogram with all four sides of equal length. A square satisfies this condition (all its sides are equal). The additional property of a square is that all its angles are right angles ($90^\circ$). This specific angle requirement makes the square a 'special' type of rhombus.
(d) Squares, rectangles, parallelograms are all quadrilaterals.
Reason: A quadrilateral is defined as a polygon with four sides. Squares, rectangles, and parallelograms are all closed figures made up of four line segments (sides). Therefore, they all fit the definition of a quadrilateral.
(e) Square is also a parallelogram.
Reason: A parallelogram is a quadrilateral whose opposite sides are parallel and equal. A square has opposite sides that are parallel and equal in length. Therefore, a square satisfies the definition and properties of a parallelogram.
Question 3. A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Answer:
Definition of a Regular Figure:
A figure is called regular if it satisfies two conditions:
1. All of its sides are equal in length.
2. All of its angles are equal in measure.
Identifying the Regular Quadrilateral:
We need to find a quadrilateral (a four-sided polygon) that meets both conditions mentioned above.
Let's consider common quadrilaterals:
Condition 1: All sides equal in length.
Quadrilaterals with all sides equal are the rhombus and the square.
Condition 2: All angles equal in measure.
A quadrilateral has 4 angles, and the sum of these angles is $360^\circ$. If all angles are equal, each angle must measure $\frac{360^\circ}{4} = 90^\circ$.
Quadrilaterals with all angles equal to $90^\circ$ are the rectangle and the square.
Combining both conditions:
We are looking for a quadrilateral that has both all sides equal and all angles equal.
Comparing the lists from Condition 1 and Condition 2:
- Quadrilaterals with equal sides: Rhombus, Square.
- Quadrilaterals with equal angles ($90^\circ$): Rectangle, Square.
The only quadrilateral that appears in both lists is the square.
Conclusion:
A square has all four sides equal in length and all four angles equal in measure ($90^\circ$).
Therefore, the regular quadrilateral is the square.
Exercise 5.8
Question 1. Examine whether the following are polygons. If any one among them is not, say why?
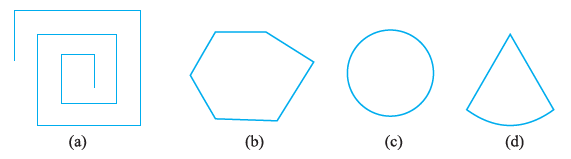
Answer:
A polygon is defined as a simple closed figure made up entirely of line segments.
Let's examine each figure based on this definition:
(a)
Analysis: This figure is made up of line segments and is simple (segments don't cross). However, it is not closed; there is an opening.
Conclusion: Not a polygon because it is not a closed figure.
(b)
Analysis: This figure is made up entirely of line segments. It is a closed figure. It is simple (segments only meet at endpoints).
Conclusion: Yes, it is a polygon. (It is a hexagon).
(c)
Analysis: This figure is a circle. It is simple and closed.
Conclusion: Not a polygon because it is not made up of line segments; it is a curve.
(d)
Analysis: This figure has two line segments and one curved segment. It is closed and simple.
Conclusion: Not a polygon because it is not made up entirely of line segments (it includes a curve).
Question 2. Name each polygon.
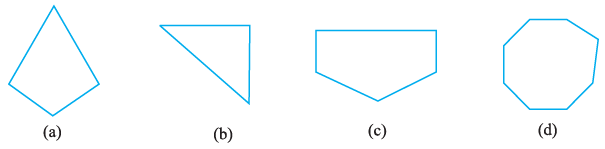
Make two more examples of each of these.
Answer:
Polygons are named based on the number of sides they have.
(a)
Analysis: The polygon has 4 sides.
Name: Quadrilateral.
Two more examples: Square, Rectangle (or any other four-sided closed figure made of line segments).
(b)
Analysis: The polygon has 3 sides.
Name: Triangle.
Two more examples: Right-angled triangle, Equilateral triangle (or any other three-sided closed figure made of line segments).
(c)
Analysis: The polygon has 5 sides.
Name: Pentagon.
Two more examples: A regular pentagon (like the shape of the Pentagon building), an irregular pentagon (any five-sided closed figure made of line segments).
(d)
Analysis: The polygon has 8 sides.
Name: Octagon.
Two more examples: A stop sign shape (regular octagon), an irregular octagon (any eight-sided closed figure made of line segments).
Question 3. Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.
Answer:
1. Rough Sketch of a Regular Hexagon:
A regular hexagon is a polygon with 6 equal sides and 6 equal interior angles. Let the vertices be labeled A, B, C, D, E, F.
2. Connecting Three Vertices to Form a Triangle:
We can form different types of triangles depending on which three vertices are connected.
Case 1: Connecting alternate vertices (A, C, E)
When we connect the alternate vertices A, C, and E, we form $\triangle ACE$. In a regular hexagon, the diagonals that connect alternate vertices are all equal in length. Therefore, $AC = CE = EA$.
The resulting triangle is an Equilateral triangle.
Case 2: Connecting three consecutive vertices (A, B, C)
When we connect three consecutive vertices A, B, and C, we form $\triangle ABC$. Two sides, $\overline{AB}$ and $\overline{BC}$, are sides of the hexagon, so they are equal. The angle at the common vertex, $\angle ABC$, is an interior angle of the regular hexagon, which is $120^\circ$.
The resulting triangle is an Isosceles Obtuse-angled triangle.
Case 3: Connecting vertices A, B, and D
When we connect vertices A, B, and D, we form $\triangle ABD$. The angle $\angle ABD$ is $90^\circ$ and the sides $\overline{AB}$, $\overline{BD}$, and $\overline{DA}$ are all of different lengths.
The resulting triangle is a Right-angled Scalene triangle.
Question 4. Draw a rough sketch of a regular octagon. (Use squared paper if you wish). Draw a rectangle by joining exactly four of the vertices of the octagon.
Answer:
1. Sketching a Regular Octagon:
A regular octagon is a polygon with 8 equal sides and 8 equal interior angles. A rough sketch is shown below with vertices labeled A, B, C, D, E, F, G, H.
2. Drawing a Rectangle by Joining Four Vertices:
To form a rectangle, we need to join four vertices in such a way that opposite sides are equal and parallel, and all angles are right angles. One way to do this is by connecting vertices that are symmetrically opposite.
For example, if we join the vertices B, C, F, and G, we get a rectangle.
In the figure above, the quadrilateral BCFG is a rectangle formed by joining four of the vertices of the regular octagon.
Question 5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
Answer:
1. Rough Sketch of a Pentagon:
A pentagon is a polygon with 5 sides and 5 vertices. A rough sketch of a pentagon ABCDE is shown below.
2. Drawing the Diagonals:
A diagonal is a line segment that joins any two non-adjacent vertices of the polygon. For the pentagon ABCDE, we can draw the diagonals by connecting each vertex to the vertices that are not its immediate neighbours.
The diagonals are:
- From vertex A: $\overline{AC}$ and $\overline{AD}$
- From vertex B: $\overline{BD}$ and $\overline{BE}$
- From vertex C: $\overline{CE}$ (and $\overline{CA}$, which is the same as $\overline{AC}$)
In total, a pentagon has 5 diagonals. The rough sketch of the pentagon with all its diagonals drawn is shown below. The diagonals form a star shape in the interior.
Exercise 5.9
Question 1. Match the following :
| (a) Cone | (i)
.png)
|
| (b) Sphere | (ii)
.png)
|
| (c) Cylinder | (iii)
.png)
|
| (d) Cuboid | (iv)
.png)
|
| (e) Pyramid | (v)
.png)
|
Give two new examples of each shape.
Answer:
Matches:
(a) Cone $\leftrightarrow$ (ii)
(b) Sphere $\leftrightarrow$ (iv)
(c) Cylinder $\leftrightarrow$ (v)
(d) Cuboid $\leftrightarrow$ (iii)
(e) Pyramid $\leftrightarrow$ (i)
Two New Examples of Each Shape:
(a) Cone:
1. An ice cream cone
2. A conical tent
(b) Sphere:
1. A football
2. A globe
(c) Cylinder:
1. A pipe
2. A can of soda
(d) Cuboid:
1. A matchbox
2. A brick
(e) Pyramid:
1. The Great Pyramids of Egypt
2. A Rubik's pyramid
Question 2. What shape is
(a) Your instrument box?
(b) A brick?
(c) A match box?
(d) A road-roller?
(e) A sweet laddu?
Answer:
(a) Your instrument box?
An instrument box (geometry box) typically has the shape of a rectangular prism.
Shape: Cuboid.
(b) A brick?
A brick is shaped like a rectangular prism.
Shape: Cuboid.
(c) A match box?
A match box is also shaped like a rectangular prism.
Shape: Cuboid.
(d) A road-roller?
The main rolling part of a road-roller has a circular base and uniform height.
Shape: Cylinder.
(e) A sweet laddu?
A sweet laddu is typically round, like a ball.
Shape: Sphere.

